Problem 15:

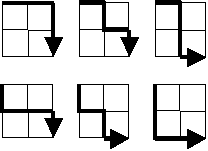
Starting in the top left corner of a 22 grid, there are 6 routes (without backtracking) to the bottom right corner.

How many routes are there through a 2020 grid?

Running time: 0ms

Assessment: I was totally lost on this problem, and I eventually had to search for some clue as to how to solve it. Once I learned it was an n-choose-k problem, it was a lot easier. I used the simplified binomial coefficient algorithm described in the Wikipedia article, but only after making sure I understood what was going on and why it was used.

This simplified method ensures you don’t overflow your primitives when calculating factorials, and it’s ridiculously fast. (As I recall, it’s much faster than the ideal solution posted by the project admins.)

In retrospect, it seems obvious that it’s a combinatorics problem, because you can’t go backwards or up, but that wasn’t apparent to me when I started.

public class Problem015
{
	public static long binomialCoefficient(int n, int k)
	{
		/* N-choose-k combinatorics: (n! / (k! * (n-k)!)
		 * Where:
		 * 		n is the number of moves,
		 * 		k is the number of down and right moves required (20 each) */

		if (k > (n-k))
			k = n - k;
		
		long c = 1;
		
		for (int i = 0; i < k; i++)
		{
			c = c * (n-i);
			c = c / (i+1);			
		}
		
		return c;
	}
	
	public static void main (String[] args)
	{
		long begin = System.currentTimeMillis();
		
		System.out.println(binomialCoefficient(40,20));
		
		long end = System.currentTimeMillis();
		System.out.println(end-begin + "ms");		
	}
}